advertisement
Rasa penasaran menghantui bang Habib setelah memikirkan bidang cartesius lama-lama. Begini kira-kira self dialognya.
Habib1: Wah hebat juga bidang cartesius ini ya, dulu aku pikir yang bisa digambar disini cuma garis lurus, ternyata ada juga persamaan yang menunjukkan grafik lengkung tak hingga (fungsi kuadrat dan akarnya)
Habib2: Iya aku salut juga, dulu aku tak pernah membayangkan bisa menggambar lingkaran disini, ternyata persamaannya x2 + y2 = r2. Kreatif juga yang menemukan!
Habib3: Awalnya aku juga kagum, tapi aku kecewa ternyata grafik polinom cuma lengkung-lengkung sebanyak pangkatnya. Yah jadinya cuma mirip grafik sinuslah.
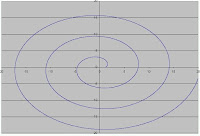
Habib Asli: Hei aku ada ide, gimana kalau kita cari grafik spiral, belum pernah dengar kan?
Akhirnya semua bang Habib bekerja sama berusaha mencari tahu bagaimana fungsi grafik spiral.
Setelah lama berpikir mereka berhasil menemukannya, begini ceritanya
Habib1: Hei ini tak mungkin! Spiral punya banyak potongan pada satu garis x bilangan Real,
Habib2: Jarak antara titik-titik yang kudapat di garis x=1 pun semakin kecil jika menjauhi pusat tapi tak menunjukkan pola-pola tertentu.
Habib3: Tetap bekerja teman-teman!
Habib Asli: Sepertinya terlalu aneh, spiral tetap punya pola. Siapa yang bisa bilang polanya?
Habib2: Aku tahu pak! Panjang jari-jarinya naik secara linier sesuai sudut yang ditempuh garis itu pak!
Habib1: Jelaskan aku tak mengerti!
Habib3: Aku paham, begini, anggaplah kau sedang membuat lingkaran dengan jangka, tapi jangka itu jangka mesin, setiap kau putar 900 jari-jarinya bertambah 1cm atau berapapun kau suka, maka dalam 1 putaran kau akan mendapati selisih jari-jari 4cm. Dan mendapatkan spiral smooth yang jari-jarinya naik terus-menerus.
Habib Asli: Kalian tahu apa artinya itu anak-anak? Artinya, kita tak bisa membuatnya secara langsung di cartesius. Kita buat rancangan awalnya di koordinat polar lalu kita terjemahkan ke koordinat cartesius.
Ternyata membuatnya di koordinat polar sangat mudah, mereka mendapati r = k . a/3600
Habib Asli: OK sempuna! Anak-anak berikan aku formula transformasi koordinat polar dan cartesius!
Habib1: Ini pak, dalam koordinat cartesius (r,a) berarti (akar x2 + y2 , arctan x/y) polar
Habib Asli: dengan kata lain x,y dalam koordinat cartesius adalah (r.cosa , r.sina)
berarti persamaan menjadi akar x2 + y2 = arc tan x/y …tankan kedua sisi, tan akar = x/y
Habib3: sampai disini tidakbisa disederhanakan lagi, pak!
Habib Asli: tak apa rasa ingin tahuku sudah terpuaskan.
Habib2: bolehkah saya dilatasi dan transisi pak,
Habib Asli: boleh ubah dari awal polarnya untuk lebih amannya
Habib2: ya pak
Misi selesai akhirnya bang habib pun bisa tidur dengan tenang, tapi dihantui persamaan spiral misterius lagi.